FAJ: 追涨不可取，而止损第一条

　　炒股就看金麒麟分析师研报，权威，专业，及时，全面，助您挖掘潜力主题机会！

　　来源：北京金融分析师协会

　　* 此项目由CFA Institute及CFA Society Beijing联合推出。

　　The Financial Analysts Journal 创刊于1945年，是CFA Institute主办的投资管理领域专业期刊。2020年，该刊位于社会科学引文索引（SSCI）二区。本中文推介项目得到了FAJ编辑部的授权。

　　FAJ： 追涨不可取，而止损第一条

　　Nonlinear Factor Returns in the US Equity Market

　　作者：Roger Clarke， Harindra de Silva， CFA， Steven Thorley， CFA

　　综述：刘冠群，CFA

　　审校：白雪石，CFA

　　原文链接：Financial Analyst Journal，Vol.80，Issue 3 （ 点击文末“阅读全文”可查看 ）

　　推荐语

　　本文由Ensign Peak Advisors前总裁Roger Clarke博士、Allspring Global Investments投资组合经理Harindra de Silva， CFA和Marriott商学院金融学荣休教授Steven Thorley， CFA联合完成。

　　本文研究1964年至2023年间美股市场最大的1000支股票，按20年周期分为三组，重点分析最近20年的业绩表现。研究聚焦于价值、动量、小市值、低贝塔和盈利能力五个经典因子，进入非线性领域探索因子特征与风险调整后超额收益之间的关系，以及其在不同时间段上的结构变化。

　　盈利能力因子载荷最高和最低两端的股票，非线性纯化后信息比率更高。最近20年，具有一流盈利能力的股票在单位风险上所提供的主动收益超过那些位于中间段只有一般盈利能力的股票。在2004-2023年间，盈利能力因子是美股市场上表现最好的因子，也是非线性收益特征最显著的因子。长期来看，盈利能力因子也保持了强劲表现。

　　动量因子能够提供的信息比率从1964年-1983年到2004年-2023年逐步下降。在第一个20年，动量因子载荷最高和最低的股票，其信息比率都很强，尤其是在牛市；而在最近20年，牛市动量能够提供的信息比率不再明显，而熊市动量的信息比率依然很强，这意味着，追涨并不可取，但止损对于风险管理非常必要。

　　低贝塔因子与风险调整后超额收益的非线性关系，在因子正得分部分表现得更明显。前两个20年里，低贝塔因子的信息比率都很强劲。进入第三个20年后，低贝塔因子的信息比率有所下降。

　　价值因子与收益的关系最近已经表现为一条接近水平的平坦曲线，这意味着最近20年，从热门股到深度价值股，价值因子对于最终收益几乎没有影响。而“价值投资”理念一直在进化当中，价值投资并不等同于投资于价值因子。

　　小市值因子的收益曲线的非线性较为复杂，呈现为双拐点的曲线。对于中型股票，小市值因子能够发挥较好的作用。但对于大型股和小型股，小市值因子是不起作用的，这意味着，不要低配超大市值的股票，也不要高配超小市值的股票。

　　本文让我们对经典五因子的理解更为深刻了，知道了其优势和局限，愿投资者抛弃教条，灵活应对市场变化。

　　摘 要

　　我们研究了五个股票市场因子的非线性收益与特征关系：价值、动量、小市值、低贝塔和盈利能力。我们的研究使用了1964年至2023年间市值最大的1，000只美国股票的月度收益和特征数据，并重点关注过去20年的平均主动收益。除了能够简化收益生成过程的建模之外，我们发现并没有理由去假设特征与证券收益之间存在线性关系。允许非线性关系的存在，可以提高因子组合的信息比率，这些组合在非线性暴露方面对其他因子进行了中性化处理。 

　　关键词 股票市场因子，低贝塔，动量，非线性回报分析，盈利能力，量化投资组合管理，小市值，价值因子

　　披露 本文作者并未报告任何潜在的利益冲突。

　　01 引言

　　长期以来，从业者在尝试探索股票市场中的异象时，通常假设因子与收益之间存在线性关系。但如果实际上因子关系是非线性的，那么在投资组合构建中假设线性关系就会导致次优结果。本次研究探讨了美国股票市场中五个知名因子的“纯化”版本在特征与收益关系中的非线性表现。我们聚焦于最近20年（2004年至2023年）的样本，同时也研究了之前两个20年期间的数据，以展示异象的结构随时间所发生的变化。为了确保价值、动量、小市值、低贝塔和盈利能力因子组合在其他四个因子方面是“纯化”的，我们对股票之间特征与特征的关系进行了非线性调整。研究发现，盈利能力因子在股票间的收益表现出了高度的非线性，低贝塔组合中的超额收益（alpha）同样呈现高度的非线性。而在最大的1，000只股票中，小市值因子收益的非线性表现较为复杂，并在世纪之交前后发生了变化。相比之下，在过去20年中，盈利收益率的回报是线性的，在整个价值谱系中也是平坦的。

　　个股在可投资的股票市场因子方面的特征通常基于分配给每只股票的会计或统计指标。例如，小市值特征通常以市值规模的对数来衡量，并带有负号以捕捉“小”而非“大”的特性。对数转换提供了更接近正态分布的个股特征，但并未解决股票回报与市值特征之间的线性关系。另一个流行的股票市场因子——价值因子——的衡量指标通常是股票市盈率（P/E）的倒数或盈利收益率。与早期Fama和French（1993）用账面市值比（book-to-market）衡量价值类似，使用倒数主要是为了比率的数学特性。具体来说，某些股票的市盈率由于没有盈利或亏损而无法定义，且高市盈率和低市盈率的同等变化在经济上却并不等价。然而，除了能够简化收益生成过程的建模之外，没有理由假设盈利收益率或账面市值比与实际获得的证券回报之间存在线性关系。

　　关于价格动量的正负二分法已经受到了一些关注，但关于在控制类似价值和盈利能力等其他常见因子后，证券回报与动量特征之间的非线性关系的研究却较为少见。对于任何一个给定的因子，一个特征得分为2.0的股票，其平均主动回报是否就是一个得分为1.0的股票的两倍？一个特征得分为-1.0的股票，其主动回报是否为相同幅度的负值？De Boer（2020）、Zhang（2022）、Bollerslev、Patton和Quaedvlieg（2023）、Kagkadis等人（2023）以及Didisheim等人（2024）的研究为近期关于股票市场中非线性回报的发现提供了背景支持。

　　本研究针对5个广为人知的股票市场因子纯化版本的收益-特征关系中的非线性进行了系统性检验。研究数据集涵盖了1964年至2023年间每月市值最大的1000只美国股票，重点关注最近20年（2004年至2023年）的数据。本研究收集的特征数据是关于5个在时间变迁中涌现的流行股票市场因子的特征数据：价值、动量、小市值、低贝塔和盈利能力。研究起始日期和因子选择基于CRSP和Compustat数据库中至少1000只个股的整体收益和特征数据的可用性。我们使用过去一年的盈利收益率来衡量价值因子，使用Carhart（1997）提出的前一年收益率减去前一个月收益率的对数形式来衡量动量因子，使用月初市值的负对数来衡量小市值因子，使用1减去过去36个月的标普500指数贝塔值来衡量低贝塔因子。盈利能力因子的特征采用的是前一年的毛利率，由Novy-Marx（2013）提出，并根据Clarke、de Silva和Thorley（2020）的描述进行了资产调整，以适用于金融类股票。

　　价值因子和市值因子在学术文献中有着广泛的研究记录，最早由Fama和French（1992）提出，尽管我们的不同是在于使用了从业者定义的盈利收益率而非账面市值比来作为价值因子指标。动量因子由Jegadeesh（1990）以及Jegadeesh和Titman（1993）引入，其不对称属性由Barroso和Santa-Clara（2015）进行了讨论，而Ehsani和Linnainmaa（2020）则探讨了动量因子与其他因子的关系。低贝塔异象隐含在早期的资本资产定价模型（CAPM）研究中，并由于Frazzini和Pedersen（2014）的研究在近年来更为流行。我们使用低贝塔作为“低波动”因子，它更精确并且具有与投资组合相关的特征。Novy-Marx（2013）将盈利能力因子引入学术文献。正如Hsu、Kalesnik和Kose（2019）所展示的，从业者所定义的“质量”首先取决于毛利率，因此对质量因子感兴趣的读者可以从盈利能力特征中推断出相关信息。

　　Sharpe（1964）以及Jensen、Black和Scholes（1972）提出的基本均衡经济学理论首先提出了这样一种理念，即那些与市场相对表现正相关的因子也必然代表了承担系统性风险所带来的回报。相反的，当今的大多数金融经济学家则相信，具有显著正向的长期阿尔法的因子是信息性或行为性的异象，这些异象尚未或无法被套利消除，比如Shliefer和Vishney（1997）的研究。另一些人则担心，部分历史结果是在“因子动物园”中数据挖掘的产物，这一点在Feng、Giglio和Xiu（2020）等研究中得到了探讨。我们通过研究在世纪之交之前就已广受欢迎的因子来缓解事后数据挖掘的问题，并采用最初的原创学术研究者提出的股票特征定义（除价值因子外）。

　　本研究首要关注的是股票间收益-特征关系的非线性，但我们也探讨了股票间特征-特征关系的非线性。我们报告了构建的最优单一因子纯化投资组合的业绩表现，这些组合剔除了与其他因子的线性和非线性关系。我们的研究使用市值加权的Fama-Macbeth回归，提供了纯化组合收益的表格以及组合内收益-特征关系的非线性可视化展示。对证券收益与特征进行的月度横截面回归是多变量的，自发的纳入所有五个因子，包括正交化的二次方和三次方特征项以捕捉非线性关系。此外，我们还通过将每个因子的证券特征分为正负值以及绝对值大于一的情况，定义了四个类别组合来检验非线性。我们对非纯因子、线性纯因子和完全纯因子类别的结果进行比较，更好的理解了收益中非线性的来源。

　　在剔除特征-特征关系的非线性后，研究发现某些因子存在经济上和统计上都很显著的收益-特征非线性关系。最复杂的非线性平均收益模式出现在市值因子区间中，而在过去20年里，毛利率和市场贝塔值在收益上也表现出非线性。在本研究中，市值敞口是在美国最大的1000只股票中相对而言的。在这个范围之外的股票流动性较低，市值的显著性较小，因此被排除在分析之外。尽管之前有大量的研究都是关于动量因子的收益拐点，但动量因子纯化版本的收益-特征关系更接近线性。在过去20年中，盈利能力因子不仅是表现最好的因子，也是非线性收益特征最显著的因子。遗憾的是，价值因子在整个敞口范围内的平均收益接近于零。换句话说，过去20年中，价值因子的收益呈线性但平坦，从热门股票到深度价值股票，价值因子几乎没有影响。

　　02 线性因子组合回报

　　在这一小节中介绍了贯穿本文的计量经济学方法，包括多元线性回归，随后展示了非线性三次回归的结果。Fama和MacBeth（1973）五因子线性回归模型的设定如下：

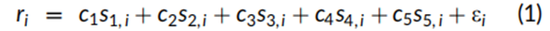
　　其中ri是从1到1000只股票一个月的证券回报，sk，i是每月初始k=1到5各因子的特征分数。横截面回归的观测值按照月初证券市值进行加权，具体原因在技术附录中有详细说明。方程（1）左侧的证券收益是主动收益，即相对于市场收益的差异收益，尽管使用总收益和截距项不会影响系数。使用总收益要在方程（1）中包含截距项c0，由于回归中的市值权重，截距项c0代表每月的市场组合收益。

　　方程（1）中的五组分值sk，i是标准化后的特征值，分别对应盈利收益率（即过去市盈率的倒数）、对数价格动量、市值的负对数、过去36个月市场贝塔值的负数以及前一年的毛利率。这些特征值每月在横截面上都是标准化的，标准化为加权均值为零、方差为一的变量，具体方法如技术附录所述。为简化符号表示，方程（1）未加入时间下标t，因为每次横截面回归的敞口数据均取自一个特定时间点，即每月的月初。加权回归的一个属性是，可以通过估计的系数推断出生成因子收益的投资组合中证券的构成。如技术附录所示，方程（1）中的估计系数代表了最优构建的单一因子投资组合的主动收益（即相对于市场的差异收益）。这些因子投资组合是完全投资的，主要由证券的多头头寸组成，与许多学术研究中用于检验因子的多空组合有所不同。

　　与Fama-French风格的因子仅对市值特征进行部分中性化不同，本文中的五个纯单一因子投资组合对其他四个特征的线性和非线性敞口均进行了中性化处理，具体方法如Clarke、de Silva和Thorley（2017）所述。在实践中，建立在纯单一因子投资组合的多因子策略几乎不包含做空操作，因为每只证券的各个因子之间已相互抵消，并减少了投入到任一单一因子中的主动风险。因此，多因子投资组合可以是纯多头组合，或者在不显著影响业绩表现的情况下被约束为纯多头组合。我们捕捉了方程（1）中的月度投资组合收益或回归系数，然后基于已实现的信息比率（IRs），使用系数标准差和经济显著性进行统计推断，来总结出过去20年（即120个月）中每个因子的平均收益。

　　表1报告了将方程（1）应用于2004年1月至2023年12月共120个月数据后的结果，其中第一列为市场收益减去同期无风险利率（一个月国库券利率）的超额收益。表1中的月度收益进行了年化处理，将平均收益乘以12，将收益标准差乘以12的平方根。例如，第一列显示，过去20年的平均超额市场收益为9.33%，标准差为15.01%，夏普比率（均值除以标准差）为0.622。表1中其他五列的夏普比率是基于主动收益计算的，不同于更常见的超额收益除以超额收益标准差的夏普比率定义。在接下来的五列中展示的纯主动收益，由于方程（1）中证券特征的标准化评分，对目标因子具有一个标准差的暴露，导致各因子之间的风险差异较显著。例如，价值组合的主动收益标准差为2.56%，而动量组合的主动收益标准差几乎翻倍，达到4.75%。

　　正如现在广泛报道的那样，在过去的二十年里价值因子组合的业绩表现已经几乎不存在了，年化的回报只有-14个bps，如表1的第一行所示。

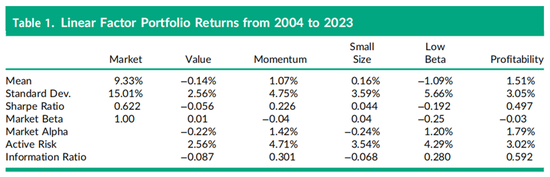
　　在并未经过对其他因子中性化处理的非纯化的价值组合（未展示）中，业绩表现更为糟糕。具体而言，仅将价值因子特征放在方程（1）右侧的非纯化价值因子的平均主动回报为-0.75%，而纯化价值因子的平均主动回报为-0.14%。非纯化的价值因子组合表现更差的一个原因是该因子特征与盈利能力因子特征之间存在负相关关系，而在过去的20年间盈利能力因子表现很好。但通常来说，正如信息比率所衡量的那样，对于所有五个因子而言，非纯化的组合都表现更差，原因是对其他因子的非中性化暴露导致回报的标准差更高。

　　每个纯化因子组合实际实现的主动市场贝塔值展示在表1的第4行。比如，价值因子组合的主动贝塔值为0.01，近乎于0，这意味着整个组合的实际市场贝塔值为1.00+0.01=1.0，略略大于1。其他因子的总贝塔值也都接近于1，除了本身设计上就倾向于低贝塔值股票的低贝塔值因子组合之外。在表1中低贝塔因子组合的市场贝塔值为1.00-0.25=0.75，该组合用主动回报减去主动贝塔值与市场回报乘积之差计算的阿尔法，为1.2%。表1中其他的阿尔法计算都接近于该因子的平均主动回报。例如，价值因子的阿尔法值为-22个bps，略低于-14个bps的平均回报，这里面轻微的差异主要源于市场贝塔值略高于1。

　　表1的倒数第二行中展示的主动风险使用了实际市场贝塔值，换句话说，即阿尔法回报的标准差。最后一行中每个因子的信息比率（IR）是用阿尔法除以主动风险计算的。盈利能力因子组合的信息比率为0.592，几乎是动量因子组合和低贝塔因子组合信息比率（分别为0.301和0.280）的两倍。与价值因子组合类似，线性的小市值因子组合的阿尔法在过去20年中略为负值，导致其信息比率为负。信息比率衡量经济显著性，而且最好与其他因子信息比率的幅度进行比较来评估。为了检验阿尔法的统计显著性，年化的信息比率可以乘以年数的平方根（本例中为20年），得到零假设（实际阿尔法为零）的t统计值。表1中纯线性盈利能力因子的阿尔法的t统计量为0.592乘以20的平方根≈2.6，因此具有显著性（即大于2.0），而其他四个因子的t统计量表明其统计上不显著。

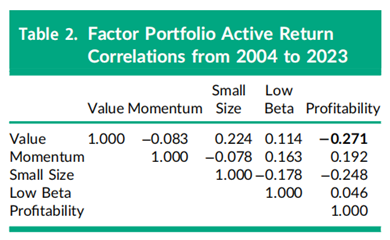
　　一个最优的多因子投资组合可以以最大化组合的信息比率（IR）为目标，通过赋予单个因子纯化组合不同的权重来构建。正如Clarke、de Silva和Thorley（2020年）所述，在因子回报不相关的假设下，这些权重与单因子投资组合的信息比率成正比。最优的五因子投资组合（未在表1中展示）的阿尔法为1.44%，主动风险为2.06%，信息比率为0.698。这一多因子组合的信息比率略低于用Sharpe信息比率近似公式（方程（2））计算的0.729，这是由于表2中报告的实际回报之间存在非零相关性。例如，尽管价值因子组合和盈利能力因子组合来自同一线性回归，但两者的实际回报相关性为-0.271。

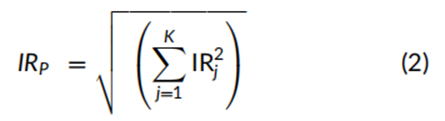
　　回报之间的时间序列相关性低于由方程（1）生成的非纯因子投资组合（即仅在方程右侧使用一个得分集构建的投资组合）的相关性，但这些相关性并不为零。例如，非纯化价值因子组合和非纯化盈利能力因子组合之间的回报相关性（未在表2中展示）为-0.312，而纯因子投资组合的相关性为-0.271。非纯投资组合之间相关性值最大的是盈利能力因子组合与小市值因子组合之间的-0.579，而表2中报告的纯因子投资组合的相关性为-0.248。表2中的相关系数绝对值大于四个标准误差（即4 × （1/240）^（1/2） ≈ 0.258）的，用粗体显示来强调。

　　03 非线性因子组合回报

　　因子组合内部的非线性回报通过扩展方程（1）来计算，扩展后的方程包括每个因子的特征得分的正交化平方和立方。非纯化单因子投资组合的回归模型设定如下：

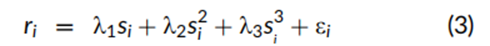
　　其中，si是特征得分，si2是基于特征的平方项。如技术附录中所述，特征平方项与线性得分经过解析正交化处理，在横截面上不相关。特征立方项si3则同时与线性得分和特征平方项正交化。方程（3）中的平方项和立方项在正交化后重新进行得分处理，使其加权均值为零，加权方差为一。正交化过程提高了检验非线性回报模式的精确性，因为如果不进行正交化，方程右端的变量之间会高度相关，从而导致实际投资组合回报之间的相关性增大。具体来说，方程（3）中的斜率系数 λ1、 λ2 和 λ3可以通过三个单独的单变量回归等效估计。与方程（1）类似，如果包含截距项，则截距项恰好为零；如果在左侧使用总证券回报，则截距项等于市场投资组合的回报。

　　表3报告了一个类似于方程（3）的回归结果，右侧包含15个变量，其中包括五个因子的特征得分及其正交化后的平方项和立方项。为了节省空间，表3并未包含回报的均值和标准差，但报告了表1中的其他行内容。例如，价值因子组合的纯线性得分系数的平均阿尔法为-32个基点，而特征平方项的阿尔法为36个基点，特征立方项的阿尔法为20个基点。在一个标准差暴露的约束条件下，三个价值因子投资组合的主动风险分别为2.47%、1.61%和1.58%，从而导致这三个价值因子组合的信息比率（IR）相对较小，分别为-0.128、0.225和0.127。

　　可以通过将每个因子的线性、平方和立方投资组合合并起来，构建一个事后最优非线性因子投资组合。表3中的“合并”列使用了每个因子的三个回报列，并使其权重之和为±100%。合并投资组合中的权重接近于三个单独投资组合的夏普比率相对幅度乘以表4中报告的逆回报相关系数矩阵。例如，价值因子的非线性投资组合回报中，得分投资组合回报的权重为-28%，平方投资组合回报的权重为98%，立方投资组合回报的权重为30%。然后，将合并后的非线性因子投资组合规模进行调整，使其与表1中相应线性投资组合的主动风险水平相等。非线性价值因子组合中最大的贡献来自于平方项，其合并非线性价值因子组合的信息比率（IR）为0.268。相比之下，非线性动量因子组合中最大的贡献来自立方项，其信息比率为0.624。小规模因子的立方权重为-66%，平方权重为-33%，其合并非线性投资组合的信息比率为0.396。

　　表3中的低贝塔因子在立方组合（cubed portfolio）上有一个较大的权重，为-143%，而得分组合（score portfolio）的权重为50%，这使得合并非线性因子组合的信息比率（IR）达到0.457。非线性盈利能力组合结合了-88%的平方组合（squared portfolio）和-36%的立方组合，并由线性得分组合的24%抵消，从而形成了一个信息比率高达0.812的合并非线性盈利能力因子组合。换句话说，在过去的20年里，非线性盈利能力因子组合实现了2.45%的显著阿尔法（alpha），而其主动风险（active risk）仅略高于3%。

　　对因子收益非线性的统计检验可以基于每个因子的平方项或立方项年化阿尔法的t统计量，其计算方法为信息比率（IR）乘以20年的平方根。例如，立方动量因子组合的t统计量为 0.544×201/2=2.4，而符号变化后的平方盈利能力因子组合的t统计量为 0.723×201/2=3.2。然而，对非线性的完整检验是基于非线性IR相对于线性IR的提升。

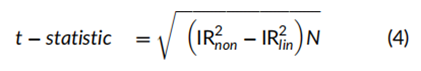
　　其中，IRnon 是表3中合并非线性组合的信息比率，而 IRlin 来自表1中线性组合的信息比率。例如，价值因子非线性的t统计量通过公式（4）计算为 （（0.2682−0.0872）×20）1/2=1.2。对其他因子的完整非线性收益检验得出的t统计量分别为：动量因子的为2.4，小市值因子的为1.8，低贝塔因子的为2.4，盈利能力因子的为4.5。因此，动量因子组合和低贝塔因子组合的收益非线性在10%的显著性水平上（即t统计量大于或等于2.0）具有统计显著性，而盈利能力因子组合的非线性则具有高度显著性。

　　表4报告了15个投资组合收益之间的时间序列相关性，即公式（3）中的相关系数，但右侧变量为15个而非3个。与表2类似，绝对值大于4个标准误差（即0.258）的相关性被加粗以作强调。例如，价值因子的线性得分组合与立方项得分组合之间的相关性为-0.491，相对较大；小市值因子和盈利能力因子组合内部的两组相关性也较大。另一方面，低贝塔因子组合之间的相关性相对较小，但市场贝塔组合与平方项动量因子组合之间的相关性较大，为-0.406。尽管这些时间序列的收益相关性已经相当显著，但如果在运行月度横截面回归之前没有对每个因子内的特征进行正交化处理，这些相关性会更高，某些情况下绝对值可能达到0.700至0.800。如此高的实际收益相关性使得难以确定非线性因子组合中业绩表现的来源，也难以确定最优组合中每个因子所需的权重。

　　“市场加15因子”Fama-Macbeth月度回归的结果可以通过多种方式可视化，但我们首先从最优非线性因子组合相对于市场的表现开始。图1在主动投资空间（active space）中绘制了五个合并非线性因子组合的表现，纵轴为阿尔法（alpha），横轴为主动风险（active risk）。每个组合表现的方位取决于其信息比率（IR）所对应的斜率，即连接图1中组合位置与零阿尔法、零主动风险点的直线斜率。例如，合并非线性价值因子组合的信息比率为0.268（如表3所示），而表1中线性价值组合的IR斜率为-0.087。非线性动量因子组合的信息比率为0.624，在图1中表现为右上角的组合位置，其主动风险与线性因子组合相同，均为4.71%，而线性因子组合的信息比率为0.301。

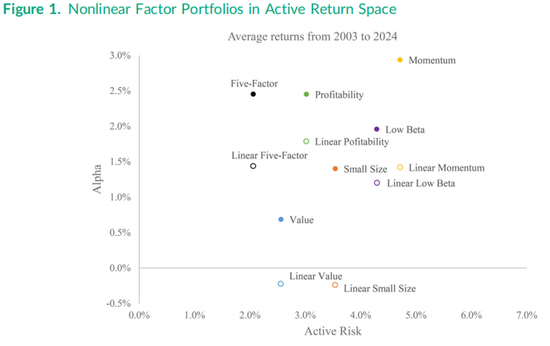
　　在图1中，小市值因子的信息比率从表1中的-0.068提升至表3中合并非线性组合的0.396，这一提升在经济意义上是显著的，尽管在统计意义上可能不显著。低贝塔因子和盈利能力因子的非线性组合信息比率分别为0.457和0.812，均优于其线性组合的表现。其中，非线性盈利能力组合的阿尔法约为2.5%，主动风险约为3.0%。图1还绘制了一个多因子组合，该组合通过将各非线性因子组合的收益按其信息比率作为权重进行构建。这个五因子组合通过最优方式（即利用收益的交叉相关性）合并了五个非线性单因子组合的表现，其出色的阿尔法表现只略低于2.5%，主动风险约为2.0%，信息比率为1.191。相比之下，最优线性五因子组合的阿尔法略低于1.5%，且主动风险水平相同。实际计算中，最优非线性五因子组合的信息比率为1.191，略低于公式（2）计算出的Sharpe规则近似值1.219，这是由于表4中报告的15个收益列之间存在非零的交叉相关性。

　　图2和图3的可视化为五个线性和非线性纯因子组合的本质提供了更多视角。图2绘制了基于表1回归结果的五个线性因子的证券主动权重，以每只证券相对于市场组合权重的比率表示。图中每个证券的点根据其2023年年中的市值大小进行缩放，以体现Fama-Macbeth横截面回归中市值加权的影响。例如，线性小市值因子组合的证券权重随着小市值得分呈线性下降，其信息比率为表1中报告的-0.068。小市值特征线上最大的两个点代表苹果（Apple）和谷歌（Alphabet），表明在线性小市值因子组合中这些股票略微超配。这两只股票在其他四个因子特征线中处于中间位置。

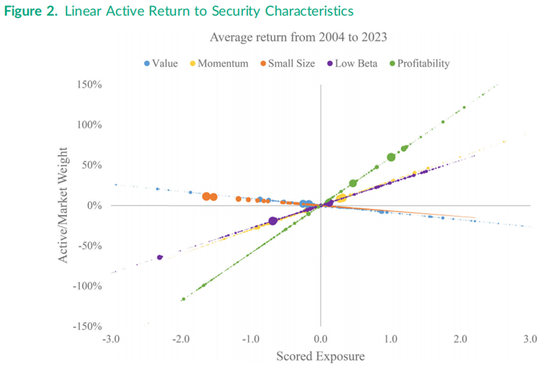
　　图2中的纵轴基于2004年至2023年的拟合非线性得分，经过缩放后，零点以上的点表示相对于市场组合的超配，零点以下的点表示相对于市场组合的低配。纵轴的调整采用了技术附录中讨论的因子组合关系：

　　其中，WM，i和 WP，i分别表示证券 i在市场组合和因子组合中的权重，si是标准化的因子特征。具体来说，拟合得分被转换为主动组合权重，即WP，i−WM，i再除以市场权重，或WP，i/WM，i−1。纵轴上的100%水平意味着主动权重是市场组合权重的两倍，而-100%水平表示主动权重为负且等于市场权重，即总权重为零。低于-100%水平的点表示在线性最优因子组合中做空的证券。例如，在线性最优盈利能力因子组合的左端，有几只证券被做空。

　　图2旨在展示关于各只证券的大量信息，包括2023年年中标准化特征的横截面分布。例如，盈利能力因子的特征分布接近正态分布，很少有证券超出-2.0到2.0的范围。相比之下，价值因子的横截面分布中有许多证券超出两个标准差的范围，而两只最大的股票——苹果和谷歌——位于分布中心的左侧。由于公式（1）中单个回归观测值的市值加权，所有五个线性因子曲线都在原点（即主动权重为零的位置）交叉。

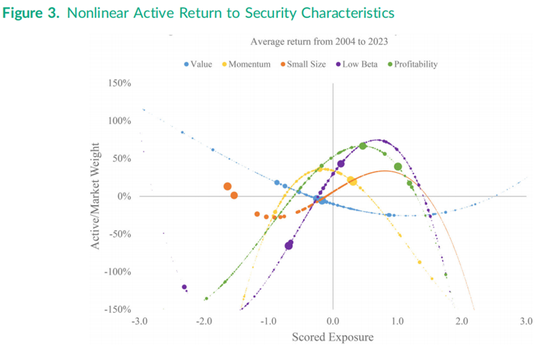
　　图3与图2类似，但展示的是表3最后一列中报告的最优非线性因子组合的表现。盈利能力因子的非线性收益呈向下抛物线形状，这主要基于平方项的高信息比率为-0.723，但其左侧尾部较为平缓。非线性低贝塔因子的收益在得分高于约1.0（即市场贝塔非常低的股票）时向下弯曲，而在图3左侧的高贝塔股票中则向上弯曲，这基于表3中报告的线性特征信息比率为0.334，立方特征信息比率为-0.346。小市值因子在图3中的形状最为复杂，主要由于立方特征的信息比率为-0.332。最大的两只股票——苹果和谷歌——在非线性小市值组合中超配，而“七巨头”（Magnificent Seven）的权重较低，随后对其他993只股票的市场相对主动权重逐渐增加，但在得分约为1.0时（即最大1000只股票中最小的股票）开始下降。需要注意的是，由于非线性函数的市值加权，图3中的曲线并未在零点交叉。动量因子呈向下抛物线形状，尽管右侧的下降趋势较弱，同时对极值负动量股票进行了做空。价值因子主要呈线性且比图2中向下的斜率更陡峭，但对于那些盈利收益率极高（即市盈率极低）的被称为“深度价值”（deep value）的股票，非线性价值因子曲线在图3中转为向上弯曲。

　　将表3中的回归结果可视化展示的另一种方式是绘制图4中所有15个组合的累积阿尔法，其中“2”代表平方特征组合，“3”代表立方特征组合。每个组合的月度阿尔法在2003年至2023年的20年间进行累积，每个阿尔法都被调整至事后3.00%的主动风险水平，以便在组合之间进行直接比较。图中盈利因子1组合在将年化风险调整后得到的阿尔法为38.25%除以20年，即1.91%，这转化为表3第一列底部给出的高信息比率（IR）1.91/3.00 = 0.638。图中下半部负数部分中更令人印象深刻的累积阿尔法来自盈利因子 2组合，其转化为表3第二列底部报告的信息比率-0.723 。这两个盈利能力因子组合的大幅正收益和大幅负收益的结合导致了图3中非线性盈利能力因子收益呈现向下的抛物线形状，而立方特征的额外贡献使得左侧的下降斜率较为平缓。

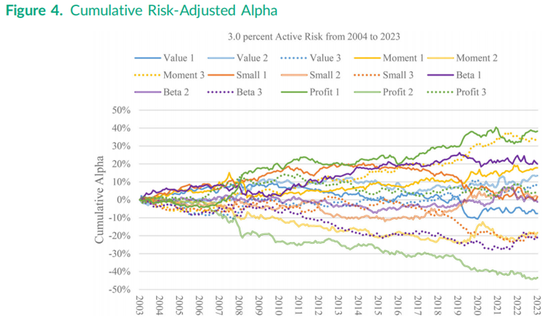
　　图4中次高的累积阿尔法是动量因子3组合，约为33%，其后是低贝塔因子 1和动量因子 1组合，均以约20%结束。图4底部也显示了较大的累积阿尔法（无论是正还是负），特别是动量因子2、小市值因子3和低贝塔因子3组合，均以约-20%结束。这些组合对应的平方动量因子、立方小市值因子和立方低贝塔因子的信息比率分别为-0.306、-0.332和-0.346，如表3所示。累积阿尔法及其相应的信息比率并未完全传达任何给定非线性因子组合的合并影响，因为三部分之间的收益相关性不为零。例如，表4中盈利能力因子1和盈利能力因子2的收益之间存在较大的负相关性（-0.497），在图4中表现得很直观，这两条曲线在2008年末之后的走势相反。

　　我们还可以使用15变量版本的公式（3）进行月度Fama-Macbeth回归，绘制比图3更精确的非线性主动收益模式。针对模拟股票的拟合主动收益每月都会生成，这些模拟股票在目标因子上的得分为-2.0到2.0之间，而其他四个因子的得分固定为零。然后，将2004年至2023年期间的240个拟合收益观测值在时间上取平均，并使用年化时间序列收益的标准差来衡量每个得分点的风险，再除以240的平方根，为平均值提供标准误差。图5绘制了每个因子从得分-2.0到2.0的平均主动收益。例如，非线性小市值因子呈现出与图3相同的双扭曲形状，而低贝塔因子曲线在右侧下降，盈利能力因子曲线在左下角显著非线性下降，这些曲线均与图3中的形状类似。值得注意的是，2004年至2023年间价值因子的拟合平均收益在图5中呈现为一条几乎完全贴着横轴的平坦曲线。

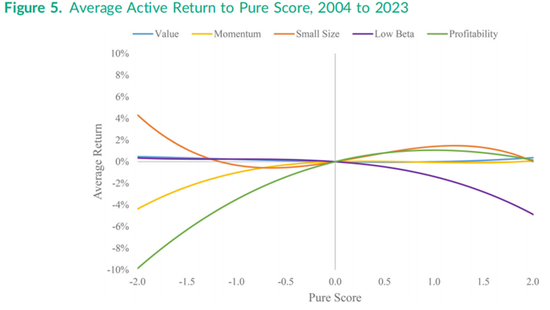
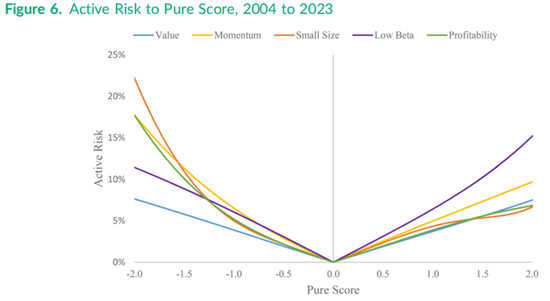
　　图6使用了与图5相同的240个拟合收益，但绘制了在目标因子每个得分点上的主动收益风险，同时将其他四个因子的得分固定为零。对于价值因子，主动风险在负得分和正得分两侧基本呈线性且对称，但对于低贝塔因子，正得分的风险略高于负得分；而对于动量因子、盈利能力因子，尤其是小市值因子，风险在得分较低的一端更高。例如，小规模因子在得分为1.0和-1.0时的风险约为5%，但对于得分约为-2.0的超大盘股，风险约为22%，是得分为2.0的最小股票风险（约7%）的三倍以上。

　　CRSP和Compustat数据库允许我们研究能够至少1000只美国股票，这些股票的特征数据完整且可追溯至1964年4月。为了涵盖完整的60年市场历史，我们将样本扩展至1964年1月至3月，尽管这三个月的横截面股票数量只有900多只。我们最初选择将整个样本分为三个20年周期，是为了在相对较长的二十年时间区间内拟合平均收益，同时允许市场动态随时间变化。事实上，240个月度相关系数平均值的背后有个关键假设，就是市场和异象结构在20年内保持一定的稳定性。

　　在本节的结尾，我们简要回顾一下之前两个20年时间段，类似于图4的累积阿尔法图以及类似于图5和图6的平均主动收益和风险图被收录于在线的前期图表附录中。这些图允许对因子收益结构在似乎发生变化时进行主观的（即非统计严格的）观察。迄今为止，在前两个时间段中表现最好的组合是基于盈利收益率衡量的价值因子组合。近年来，关于价值因子衰落的讨论很多，尽管历史上它曾是五个因子中表现最好的，但明确的给出一个“价值因子消亡”的日期则是主观的。价值因子组合的表现在世纪之交出现了一次爆发，随后在2008年金融危机之前有较小的增量表现，但自此之后纯价值因子一直处于下降趋势。与图5类似的价值因子平均收益图在前两个20年时间段中主要呈线性，但都有强劲的上升斜率。

　　在线前期图表附录中另一个值得注意的视觉变化是，小市值因子1组合的曲线在1999年左右从下降变为上升。在1984年至2003年中期，小市值因子的主动收益呈现出双扭曲形状，如图5所示，但其形状在垂直方向上翻转，使得曲线在左侧下降。盈利能力因子的非线性模式也与最近20年不同，其大部分增值来自具有正盈利能力得分的股票，而不是低配那些得分为负但平均主动收益为正的股票。1984年至2003年的低贝塔因子曲线相当线性且平坦，但在考虑传统CAPM（资本资产定价模型）中低贝塔版本的证券市场线（SML）向下倾斜后，低贝塔的阿尔法仍然是高的。有趣的是，与图5类似，大多数因子的主动收益在1964年早期至1983年间通常更为线性，除了低贝塔异象之外，其在低贝塔侧（即较大的低贝塔正分）遵循预期中的向下倾斜的SML曲线，但在高贝塔侧则不然。

　　04 证券特征之间的非线性关系

　　在本节中，我们研究了股票之间非线性的特征-特征成对关系。尽管每个因子的非线性收益-特征模式是本次研究的重点，记录特征之间的非线性关系则促使了在加权Fama-Macbeth回归中包含月初的平方和立方特征。为了构建每个因子的纯化非线性组合，需要在公式（3）中包含其他因子的平方和立方特征。图7和图8展示了当前（即2023年年中）使用横截面回归得出的盈利收益率与其他四个特征之间的关系。

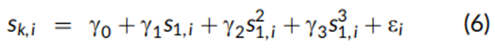
　　其中，Sk，i表示股票 i在因子 k 上的得分特征。为了分析线性关系，公式（6）中k=2到5 的应用仅包含盈利收益率得分S1，i。与公式（1）类似，由于市值加权，单变量回归中的估计截距项 γ0 恰好为零。图7将这四个成对回归的拟合得分绘制在纵轴上，而盈利收益率得分绘制在横轴上。这些线由每只股票的单点构成，许多点超出了-2.0到2.0的得分范围，这是基于盈利收益率特征在股票中的分布而成。

　　图7中最大的线性关系是盈利收益率与毛利率之间的负相关关系，表明目前较高的会计毛利率通常出现在盈利收益率较低的股票中。另一方面，盈利收益率与低贝塔特征呈正相关，表明目前高收益股票往往具有较低的市场贝塔值。图8与图7类似，但公式（6）的右侧包含了平方项和立方项。在公式（6）中，立方得分和平方得分可以正交化，但并未正交化，因为在本节中我们关注的是整体拟合效果，而非单个相关系数。

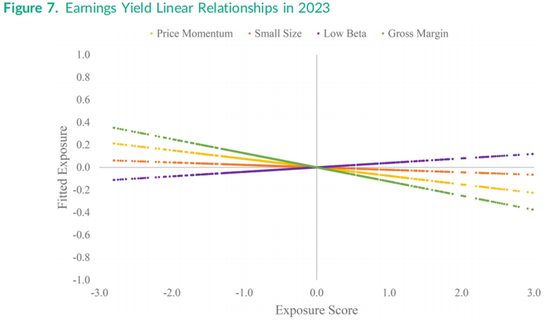
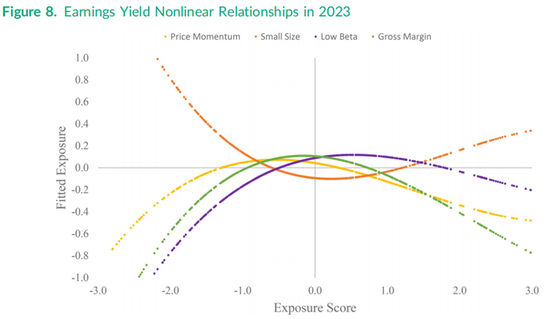
　　图8中盈利收益率与毛利率敞口之间的关系呈现高度非线性，目前最高的毛利率出现在盈利收益率中等范围的股票中。统计检验表明，在大多数月份中的大多数因子配对，线性假设都在高显著性水平上被拒绝，特别是公式（6）的平方项和立方项的系数联合为零的F检验。图8显示，当前（即2023年年中）盈利收益率相对于价格动量因子、低贝塔因子和毛利率的关系呈凹形。有趣的是，盈利收益率相对于小市值特征呈凸形，但抛物线的形状在右侧趋于平坦。

　　图9捕捉了毛利率而不是盈利收益率与其他四个特征之间当前的线性关系。需要注意的是，毛利率的横截面分布呈现正偏态，具有长右尾，这可以从图9右侧的散点图中看出，但没有散点低于−2.0。盈利收益率的拟合线呈负斜率，这再次确认了图7中这两组暴露之间的负相关关系。与毛利率线性相关性最强的是小市值特征，相关系数为−0.335，最拟合线性位于特征得分为1.0的位置。

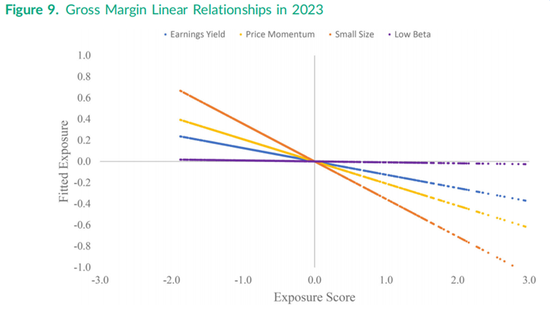
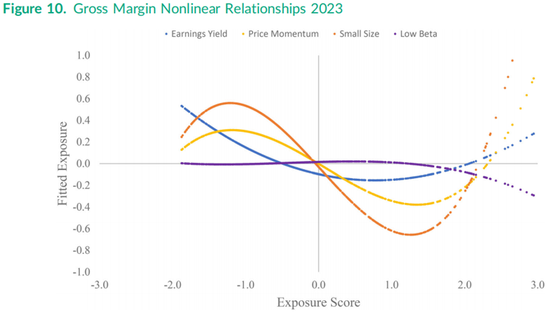
　　图10绘制了毛利率与其他四个因子之间当前的非线性关系，类似于图8中盈利收益率的关系。其中价格动量因子和小市值因子两个拟合图具有显著的立方项，导致曲线形态更为复杂，而与低贝塔特征的关系则相对线性。换句话说，在2023年，公式（6）右侧的市场贝塔的平方项和立方项相对都不那么重要。毛利率与盈利收益率的关系具有显著的二次方关系，但没有三次方系数，这与图8中盈利收益率对毛利率的反向图一致，因此图10中的盈利收益率曲线仅有一个拐点。

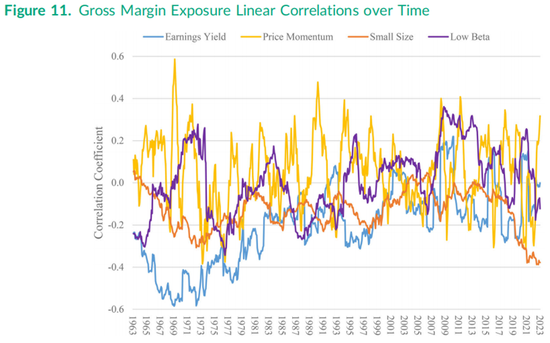
　　股票之间的非线性特征-特征关系会随着时间的推移逐渐变化，就像更为人熟知的线性关系（即相关系数）一样。具体来说，与20年前（即2003年年中）的市场相比，从相同时间点的观察视角来看，如今任何一对因子暴露之间的关系都几乎没有任何相似之处，如图8和图10所示。为了说明特征间关系的动态本质，我们在图11中聚焦于过去60年毛利率的简单线性相关性。通常与毛利率呈负相关的盈利收益率，其相关系数近几十年来在0.2到−0.2之间波动。当下（即2023年底），该相关性略微为负，这再次确认了图9中的负斜率关系，但在20世纪70年代末，这个相关性要大得多，约为−0.6。

　　如图11所示，毛利率在股票间通常与小市值特征呈负相关，这意味着市值规模较大的股票往往具有更高的财务会计毛利率。然而，当前的相关性接近−0.4，是这60年历史中迄今为止最大的数值。换句话说，盈利能力因子暴露（通常被描述为与股票间的价值因子暴露几乎相反）在当前市场中与小市值因子特征的负相关性更强。毛利率特征或其他任何特征与价格动量因子的相关性在不同股票间是不稳定的，因为动量因子特征的定义每年都会因每只股票的变化而不同。图11显示，近几十年来毛利率与低贝塔特征的相关性在0.2左右波动，但在20世纪70年代末和80年代曾达到−0.3。

　　类似于图11的其他图可以展示如小市值特征与其他四个因子之间的线性关系，以及各种非线性关系。但这些图都指向同一个实证结论：因子暴露之间的两两关系既是非线性的，也是随时间动态变化的。在股票因子研究中，关于一组特征与另一组特征之间呈现或正相关或负相关的陈述，都应被视为特定时间点的结论，而不是市场结构的永久性描述。

　　05 因子组合的类别表现

　　在这一小节中，我们使用一种不同的方法来记录因子投资组合中的非线性表现模式。与多元回归不同，我们通过构建基于因子得分的投资组合类别来研究收益与特征之间的非线性关系。将原始特征转换为得分是一个成熟且被广泛接受的流程，具体方法是减去所有N只（例如1，000只）证券的横截面均值，再除以横截面方差。在本研究中，我们使用了基准锚定的均值和方差，这意味着在计算均值和方差时采用的是期初的市场权重。如技术附录中所述，将K组（例如5组）因子暴露相对于其他K−1组暴露进行同步正交化，需要使用矩阵代数表达式：

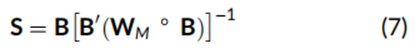
　　其中，S 是一个 N×K 的纯得分矩阵，WM 是一个市场权重向量，B是一个 N×K 的暴露矩阵，其中每个暴露值都减去了其加权平均值。从概念上讲，公式（7）右侧的矩阵 B通过方括号中显示的逆加权协方差矩阵转换为矩阵 S。需要注意的是，正交化后，由于特征集之间的非零相关性，得分必须重新调整为单位方差。

　　本文相比 Clarke、de Silva 和 Thorley（2017）的研究的创新之处在于，平方和立方特征被包含在矩阵 B 中，这使得矩阵 B 的列数从5列增加到15列，而输出矩阵 S 的前5列是完全纯化的得分。如技术附录中所述，表述平方和立方特征的列在分析上被正交化，相对于得分列以及彼此之间均分别实现了正交化，这与回归应用中的方法类似。我们将非纯得分定义为未通过公式（7）调整的标准化特征，将线性纯得分定义为矩阵 B 为5列时输出矩阵 S 的得分，将完全纯得分定义为矩阵 B 为15列时输出矩阵 S 的前5列得分。

　　对于所有三种类型的得分——非纯得分、线性纯得分和完全纯得分——构建因子投资组合的权重计算方式非常简单，

　　其中，wMi是市场权重，wPi是投资组合中第i只证券（i从1到N）的主动（即市场差异）权重。从概念上讲，公式（8）中的得分将市场投资组合权重转换为主动因子投资组合权重，这些权重的总和为零，而不是一。如技术附录中的讨论，在“市场加一个主动因子”的收益生成过程以及特质风险均为同等水平的假设下，通过公式（8）构建的单因子投资组合是均值-方差最优的。投资组合的收益通过以下求和公式每月计算：

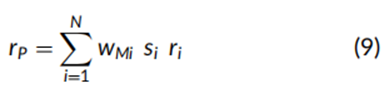
　　其中ri是证券回报。

　　在方程（9）中计算的组合回报是主动的，意味着与市场回报的差异，并且在经过了不等于1的市场贝塔额外调整（注释3所述）后用以衡量因子的表现。用方程（8）构建的因子组合并非纯多头组合，因为暴露得分小于-1的证券其实是做空的。构建严格的多头投资组合会去除因子暴露较低的一端，从而模糊了对收益与因子暴露之间非线性关系的研究。这类投资组合通常被称为120/20多空组合，意味着投资组合名义资金量的20%由做空头寸提供融资进行多头投资。与之前章节中基于回归系数的投资组合收益类似，用于做空的实际资本量会由于因子和时间段的不同而在约10%到30%之间波动。

　　表5的第一列报告了每个子期间内完全纯价值因子投资组合的总alpha，随后是包含了因子暴露得分在−1、0和1之间的证券的特征类别。具体来说，四个类别收益是将方程（9）中的总投资组合主动回报区分后的条件求和，即：

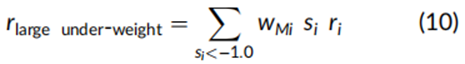
　　其他三个类别中求和的条件分别是得分范围在−1.0到0.0之间（低配类别）、0.0到1.0之间（超配类别）以及大于1.0（大幅超配类别）。这些类别本身是证券的权重由得分乘以市值决定、但未调整为完全投资的投资组合。这确保了总投资组合的alpha是四个类别投资组合alpha的简单加总，不过如果每个投资组合除以该类别的每月证券市值权重总和的情况下，这一属性将不成立。

　　我们为这四个类别赋予了因子特定的名称，这些名称借用了当前投资管理中与暴露范围相关的术语：对于盈利收益率类别，分别为热门股（得分小于−1）、昂贵股（−1到0）、浅价值股（0到1）和深度价值股（得分大于1）。表5中显示的2004年至2023年最近20年间价值投资组合只有−31个基点的alpha，将其分解后得到的类别alpha也很小，分别为14、−5、5和−45个基点，这意味着价值因子暴露谱系内存在线性关系。正如第一小节中使用Fama-Macbeth横截面回归所记录的那样，在过去20年中，价值因子谱系内的任何部分均未显著优于或劣于市场投资组合。虽然可以创建更多类别（例如五分位或十分位投资组合），并在每个类别中保持相同的资本化比例，但与市场投资组合相比超配和低配证券的自然分界线仍然是0。类似的，−1是低配而且在全谱单因子投资组合中被做空的证券的分界线。

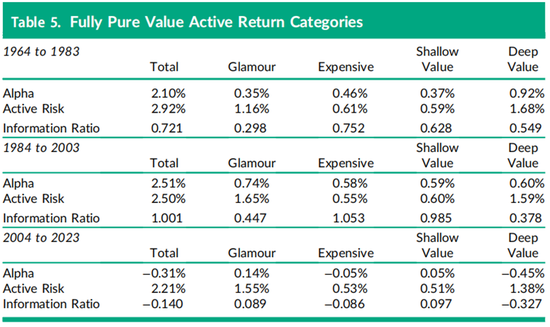
　　表5还报告了每个类别的主动风险和信息比率（IR）。需要注意的是，即使在收益与特征成线性关系的假设下，由于尾部类别（例如表5中的热门股和深度价值股）的因子暴露更大，其alpha和主动风险的数值在绝对值上也更大。在特征的横截面分布为完全正态分布的情况下，平均暴露值分别为−1.53、−0.46、0.46和1.53。因此，一般经验法则是，尾部类别的alpha和主动风险是中间类别的3倍（即1.53与0.46相比），因为它们的因子暴露大约是中间类别的三倍。例如，热门股类别的主动风险为1.55%，大约是昂贵股类别主动风险0.53%的三倍。另一方面，通过alpha除以主动风险计算的信息比率（IR）在各个类别之间具有直接可比性。

　　表6报告了表5中价值因子的信息比率（IR），以及本研究中其他四个因子的类别信息比率。表6中的因子投资组合是将完全纯得分应用于公式（8）构建而成的。对于20年年化信息比率使用1/201/2 ≈ 0.224的标准误差规则，相邻类别的信息比率在差异达到两个标准误差（即t统计量大于或等于2.0）时标记为小于（<）或大于（>）。在较早的价值投资组合收益中，统计上最显著的非线性特征是中间类别的信息比率优于尾部类别的信息比率，四对中有三对显著不同。但这种价值类别的非线性在最近20年中消失了，除了深度价值类别的信息比率为−0.327外，没有出现较大的信息比率。表6中的动量因子结果也证实了回归分析发现的最近20年期间表现下降的趋势，信息比率仅为0.352，而前面两个20年期间的信息比率分别为1.165和0.593。在第一个20年期间（1964年至1983年），动量因子的表现在尾部更强，尤其是在正动量侧，牛市类别的信息比率为0.975。这一特征在随后的20年期间（1984年至2003年）在负动量侧更为明显。在最近的20年期间（2004年至2023年），熊市和负动量类别之间的信息比率差异具有最高的统计显著性。

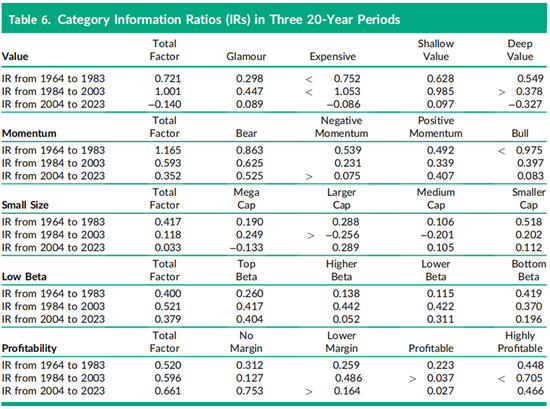
　　表6接下来报告了纯小市值因子的表现，其中现在流行的“大盘股”（mega-cap）术语与因子暴露得分低于−1的股票相关联。其他三个类别包含美国市场中最大1，000只股票中较大、中等和较小市值的股票。通常被称为小盘股的股票（例如罗素2000指数中的股票）未包含在本研究中，因此“小市值”是相对于我们自己的数据集而言的，更接近于罗素1000指数股票。在第一个20年期间（1964年至1983年），根据此定义的小市值因子表现良好，信息比率为0.417。然而，在中间的20年期间，信息比率下降至0.118，这是由于中间类别的信息比率为负，尤其是低配较大市值股票的信息比率为−0.256。然后在最近的20年期间（2004年至2023年），做空大盘股类别变得不利，信息比率为−0.133，而低配较大市值股票则变得有利可图，信息比率为0.289。相比于1984年2003年的二十年间，小市值的类别表现在过去20年（2004年至2023年）间的非线性模式发生了显著翻转：大盘股类别的信息比率从0.249下降至−0.133，而较大市值类别的信息比率从−0.256上升至0.289。

　　表6接下来报告了低贝塔因子的表现，其中标准化因子暴露得分小于−1.0的类别为超高贝塔类别，之后依次为高贝塔、低贝塔和最低贝塔，最低贝塔类别则是因子暴露得分大于1.0的类别。实际整体市场贝塔值的范围处于从低贝塔因子暴露范围的低端约1.2到暴露范围的高端约0.8之间。证券间的36个月历史贝塔特征范围略宽，从约0.6到1.4。换言之，证券贝塔值在实际值与预测值之间呈现出了出众所周知的向1收缩的现象，这一现象通常被称为Scholes和Williams（1977）修正。

　　在前两个20年期间，低贝塔因子的强劲信息比率表现引发了早期对经典资本资产定价模型（CAPM）测试的困惑。用我们的术语来说，CAPM预测低贝塔因子的信息比率应为零，但1984年至2003年的信息比率为0.521，比零高出两个标准误差以上。从1964年至1983年实证观察到的纯证券市场线（SML）不仅过于平坦，甚至出现了倒置。在第一个和第二个20年期间，各类别的信息比率表明，经典CAPM模型在实证上的失败在市场贝塔因子范围内广泛出现，但在1964年至1983年期间，最低贝塔尾部类别的差异尤为显著。

　　表6表明，与价值因子不同，盈利能力因子长期以来保持了强劲的表现，其总因子信息比率从第一个20年期间的0.520增加到0.595，然后在最近的2004年至2023年期间进一步上升至0.661。除了早期的1964年至1983年期间外，盈利能力因子最一致的非线性观察结果是信息比率表现集中在尾部类别，例如最近20年期间的0.753和0.466，而中间类别的信息比率分别为0.164和0.027。这种非线性模式与表3底部展示的盈利能力因子特征平方项的信息比率为较大的负数，即−0.723，以及非线性盈利能力因子在图3中呈现向下抛物线形状的表现一致。

　　接下来，我们探讨了使用非纯得分、线性纯得分和完全纯得分对每个因子进行线性和非线性因子投资组合纯化处理的影响。表6仅报告了完全纯得分的结果，而表7为了节省空间只包含了最近20年的数据。具体来说，表7的第一部分报告了使用简单得分特征构建的投资组合，而结果显示信息比率较低，正如Clarke、de Silva和Thorley（2017）所报告的那样。例如，2004年至2023年期间的总盈利能力因子信息比率从表6中的0.661下降到表7中的0.595。表7第一部分中几乎所有因子的总信息比率都较低，这是因为未中性化的因子投资组合受到其他因子暴露的污染，增加了主动风险，但并未增加阿尔法。在某些情况下，信息比率的下降还源自于未中性化暴露导致的阿尔法下降，从而导致与其他因子的实际收益的相关性更高。

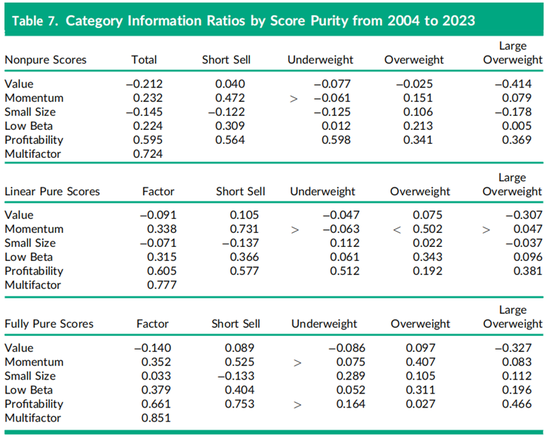
　　表7中每个总投资组合列末尾的多因子信息比率是通过Sharpe的信息比率规则（如公式（2）所示）计算出来的，衡量了所有五个投资组合的综合影响。总体发现是，随着投资组合纯度的提高，从非纯得分到线性纯得分，再到表7最后部分的完全纯得分，组合表现也会逐步提升。通过中性化因子之间的线性特征关系，多因子信息比率从0.724增加到0.777，增加了0.053；通过进一步中性化非线性关系，多因子信息比率从0.777增加到0.851，进一步增加了0.074。表7还表明，动量因子和低贝塔因子信息比率的提升主要来自线性纯化，而盈利能力因子信息比率的提升主要来自非线性纯化。

　　在表7底部部分，前面也讨论过的盈利能力因子表现在尾部类别聚集的现象，在表7中间部分的线性纯得分中不太明显，而在非纯得分构建中几乎不存在，因为在两边的尾部类别和中间类别的信息比率都几乎相等。在过去20年中，小市值因子类别也显示出显著变化，低配类别（在表6中称为较大市值类别）的信息比率从完全纯得分的0.289下降到线性纯得分的0.112，再到非纯得分的−0.125。表7表明，小市值因子和盈利能力因子投资组合的收益非线性在对其他因子的线性和非线性暴露进行中性化处理后更为明显。

　　06 非线性收益的其他应用

　　本文研究聚焦于流行的股票市场因子的平均非线性收益与特征关系。我们通过在20年的期间内拟合收益，记录下了大多数因子在统计和经济上均具有显著的非线性结构。过去，学术研究人员使用相同的事后平均收益分析来建立线性因子的表现，但样本内的拟合并不能直接解决收益可预测性的问题。Fama和French通过研究在较长时间内所实现的平均股票收益，引起了人们对线性价值因子和小市值因子的关注。选择账面市值比和对数市值特征并非由经济理论驱动，它们只是单纯反映了价值因子与市值因子作为美国股票市场重要属性的普遍认知，例如20世纪90年代引入的著名的晨星3×3图表所示。

　　事实上，唯一由均衡经济理论驱动而非事后发现的因子特征是市场贝塔因子，而经典资本资产定价模型（CAPM）的预测结果却缺乏实证支持。具体来说，高贝塔股票并未被发现具有更高的平均收益，而是与低贝塔股票的收益大致相同，这一现象现在被称为低贝塔异象。同样，本研究通过事后分析60年的收益数据，表明大多数因子在特征上具有非线性收益。本研究并未直接解决样本外的收益预测问题，尽管基于非线性模式的强度和持续性来看，这一方向具有潜力。我们曾尝试使用过去10年的非线性收益模式进行月度投资组合收益的预测，结果明确显示其表现优于线性预测，同时也探讨了如今被称为“因子动量”的方法（如Ehsani和Linnainmaa（2020）所讨论的），即使用之前三个月的收益进行预测。然而，关于直接非线性收益预测的报告超出了本文的范围。

　　本文也未涉及多因子投资组合策略的绩效归因。具体来说，可以设想一个过程，其中某个月的收益不仅可以由线性的价值因子、盈利能力因子和市值因子组合的表现解释，还可以由诸如深度价值、高盈利能力和大盘股等类别投资组合的收益来解释。事实上，市场观察者经常通过大盘股的表现来总结每日或每月的市场表现，还可以通过将大盘股作为虚拟变量进行建模。对于具有显著非线性收益的因子，主动策略的实际表现自然更多地由四个类别收益而非单一投资组合收益解释。绩效归因还可以通过加入特征的平方项和立方项来提升，如第一小节中月度Fama-Macbeth横截面回归所示。虽然非线性绩效归因超出了本文的范围，但我们简要评论了使用R平方统计量解释实际证券收益的横截面差异的传统学术目标。

　　图12绘制了本研究中整整60年期间出自包含5个右侧变量的方程（1）和市场加15个变量版本的方程（3）滚动36个月的R平方值。线性与立方项R平方图还与基于公式（1）的局部加权散点平滑回归（LOESS）的R平方图进行了对比，LOESS回归是一种允许证券收益与特征之间非线性关系采用非参数形式的方法。

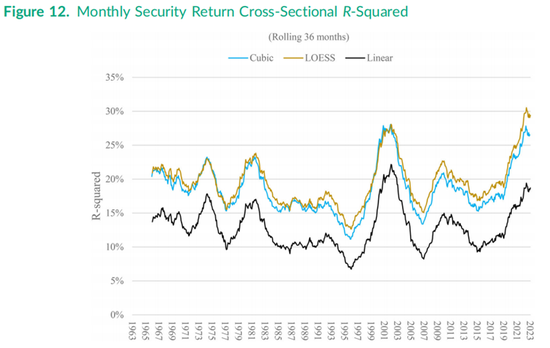
　　立方回归和LOESS回归这两种建模非线性收益的方法在36个月滚动R平方值上几乎带来了相同的提升，如图12所示，立方回归和LOESS回归的曲线高度重叠。随着时间的推移，这两种非线性收益方法都使R平方值提高了约6个百分点，尽管近年来与线性R平方值的差异已扩大至约10个百分点，如图右侧所示。具体来说，截至2023年底，LOESS回归和立方回归的R平方值分别为29%和26%，而线性R平方值仅为19%。

　　学术文献中已经发表了大量通过增加额外因子特征来提高解释力的研究，某些研究中R平方值甚至提升至30%或40%。图12中的结果表明，允许这五个流行因子的非线性，作用比增加一个甚至几个不太常用的因子要大得多。类似的，商业风险模型提供商已经开始加入平方项和立方项，特别是针对市值因子特征。

　　07 摘要与结论

　　非线性因子关系对投资者和投资组合经理的启示是重要且多方面的。通过不止是用其线性因子特征来加权证券，同时也使用横截面回归中正交化的平方和立方因子特征给出的非线性模式进行加权，投资组合的业绩表现得到了提升。表3记录了某些单因子和包含了非线性平均收益模式的多因子策略中信息比率（IR）的显著提升，在图3和图5中进行了可视化呈现。例如，过去20年中线性盈利能力投资组合的阿尔法已经高达1.79%，而在相同主动风险水平下，非线性盈利能力投资组合的阿尔法进一步增加了66个基点，达到2.45%。另一方面，对于表现不佳的价值因子，除了确保投资者构建纯价值因子投资组合以避免其与表现优异的盈利能力因子高度负相关外，似乎没有太多可做的。基于最大1，000只股票中非线性模式的小市值因子的更新版本表现更好，它低配较大市值股票但不低配大盘股，同时超配较小市值股票但不超配最小市值股票。

　　虽然我们的研究方法相比用线性版本去探索广为人知的市场异象更复杂一些，但本文的正文和技术附录提供了将非线性分析纳入投资组合构建的方法。其他研究人员也曾使用过平方和立方特征来探索收益中的非线性。我们更精确的结论正来自于我们的方法创新，即采用与线性股票特征正交化的平方和立方得分。非线性投资组合策略还受到论文中报告的因子特征类别的启发，推动了虚拟变量或分段线性回归分析及投资组合构建。对于量化分析师来说，最简单的操作可能是在其线性股票特征列表中专门加入市值因子的对数立方项和毛利率因子的平方项。

　　激发本文研究的问题是：具有2.0得分特征的股票是否能够平均实现两倍于只有1.0得分特征股票的主动收益，以及具有-1.0得分暴露的股票是否能够平均实现与得分1.0的股票相同幅度的负主动收益。对于本研究中五个流行因子中的四个，纯因子投资组合的答案是否定的。除了对非线性因子投资组合构建的影响外，本次研究结果还表明，在因子暴露谱系的某一部分增加主动权重与在谱系上移动的影响不尽相同。例如，在低贝塔异象中，通过减持贝塔略高的股票所带来的投资组合回报变化，与减持贝塔更高的股票的结果并不相同。低配主动贝塔（即相对于1的差异）为1.0的股票对投资组合回报的影响，与超配主动贝塔为-1.0的股票并不相同。在低贝塔和其他因子投资组合中，主动收益的底层来源可能会因假设的（且通常未明说的）因子暴露的线性外推而被严重误判。

　　除了发现四种流行因子的非线性收益-特征模式这一基本结论外，本研究还表明，由于高度显著的非线性成对的特征-特征模式会随着时间逐渐变化，因此不仅需要对因子暴露进行线性纯化，还需要进行非线性纯化。表7聚焦于过去20年的数据，表明了消除非线性关系带来的多因子组合业绩表现的增量提升比消除简单的线性关系系数模式带来的增量更大，尤其是对于盈利能力因子而言。我们对非线性收益的研究阐明了在横截面股票统计中锚定比较基准的必要性，如因子暴露、标准差和相关性，正如在众所周知的加权计算投资组合收益那样。基准锚定促使我们使用市值加权的月度Fama-Macbeth回归，而不是等权回归，因为等权回归产生的相关系数是非最优投资组合的，生成的收益也是相对于等权全市场组合而言的，而非与市场基准相比较的主动收益。等权回归的结果是由占股票样本80%但市值占比仅为20%的小盘股驱动的。

　　我们提到了但并未完全探讨非线性收益预测和业绩归因的问题。商业风险模型已经为某些因子引入了平方和立方特征，但非线性业绩归因只在媒体和分析师对因子表现的报道中昙花一现。例如，对美国股票市场表现的每日和月度描述中，常常都会将超大市值股票或“七巨头”作为独立的解释因素进行点评，并没有对市值谱系的其他部分进行线性外推。类似的，分析师和主动投资组合经理会谈论深度价值或魅力股策略，这些策略与中段价值谱系的简单线性外推截然不同。如图12所示，业绩归因可以显著改进，R平方值的增加证明了这一点。当人们认识到对于流行因子存在非线性的回报-因子暴露模式时，我们也会看到更好的市场点评。

　　我们对于进一步扩充“因子动物园”有所犹豫，我们注意到，20世纪90年代学术研究人员识别和强调的因子仅限于那些具有长期线性表现记录的因子。例如，在当时普遍使用的线性研究方法下，那些具有强烈非线性长期表现的垂直向下或向上抛物线平均收益股票特征，是无法被识别的。对于我们关于美国股票回报的一个重要拓展将是基于和因子组合谱系一致的非线性模式进行收益预测的方法。其他问题则需要将本文概述的非线性因子收益分析扩展到国际股票市场。CRSP和Compustat数据库仅涵盖全球公开股票市场一半左右的数据。我们预期其他研究人员会将我们的方法（包括使用正交化平方和立方特征的加权Fama-Macbeth回归）应用于欧洲和亚洲市场。在美国以外的市场里非线性的纯价值因子是否还有存在感？表现优异的纯盈利能力因子和低贝塔因子在全球市场中是否仍然具有相同的非线性特性？

　　*本文特别感谢阳光保险的郭亮博士提供技术指导。

　　Financial Analysts Journal（简称”FAJ”） 是CFA协会（CFA Institute）主办的全球知名的投资管理领域专业期刊，该刊为季刊，每期发表论文4-8篇，在社会科学引文索引（SSCI）位列二区。

　　2021年底，CFA北京协会获得了CFA Institute期刊编辑部正式授权，邀请了一批协会内外的专家和志愿者作为推荐人/审校人，启动了FAJ研究成果推广项目。

　　【项目使命】本项目定位于将期刊的优秀研究成果，尤其是对中国投资实践具有启发意义的研究成果，以中文推荐和综述的形式发布在包括不限于“北京金融分析师协会”公众号的公共平台。项目的推荐人均为在金融投资实践和学术研究方面具有一定经验和成果的专业人士，因而能够较好的将来自国际市场的学术研究成果进行中国本土化转化，揭示出对我国金融市场的学习借鉴意义，吸收国际前沿学术成果，使之融入我国金融业的高质量发展和双向对外开放历史进程。

　　截至2024年12月初，本项目已经发布研究成果50期，涉及资产配置理论前沿、ESG投资理论与实践、市场微观结构、组合构建策略、行为金融等多个领域，据不完全统计，这些研究成果的全媒体累计阅读量超过123万人次，公众号累计分享次数超4700次，包括中国人民银行主管的《金融时报》新媒体平台、财新网、新浪、凤凰等传统门户、清华金融评论、学说等学术类新媒体平台、中国保险资管业协会等行业组织公众号，都对本项目的研究成果多次关注和转载。

　　2024年6月5日，CFA北京协会FAJ中文推介项目作为“协会成功故事”被CFA Institute官方网站Connexions报道，分享给全球160余家CFA地方协会。